状态反馈和极点配置知识点总结
本文为对状态反馈和极点配置的知识点总结 ### 1、状态反馈和输出反馈
1.1 状态反馈和输出反馈
(1)状态反馈
\(\dot{x} = Ax+Bu\)
\(y=Cx\)
引入状态的线性反馈:\(u=v-Kx\)
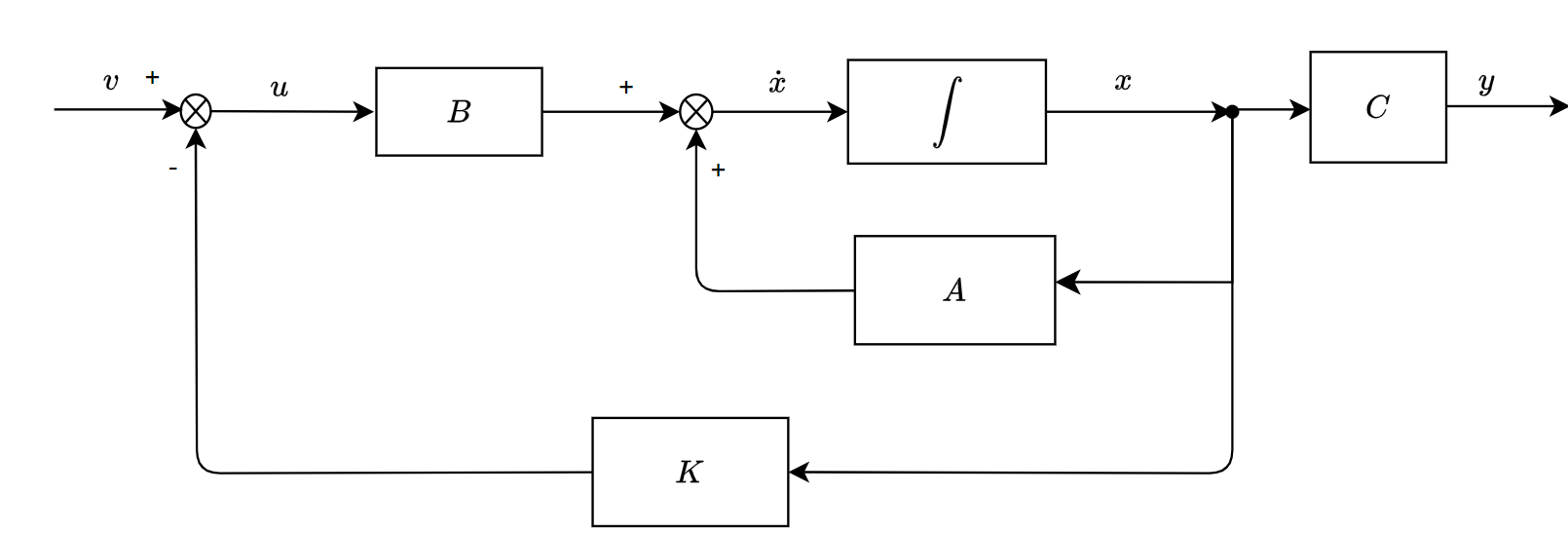
故: \[ \begin{equation} \begin{split} \dot{x}&=Ax+B(v-Kx) \\ &=(A-BK)x+Bv\\ y&=Cx\\ \end{split} \end{equation} \] 故特征多项式:\(\alpha(s)=det(sI-A+BK)\)
传递函数矩阵:\(G_k(s)=C(sI-A+BK)^{-1}B\)
(2)输出反馈
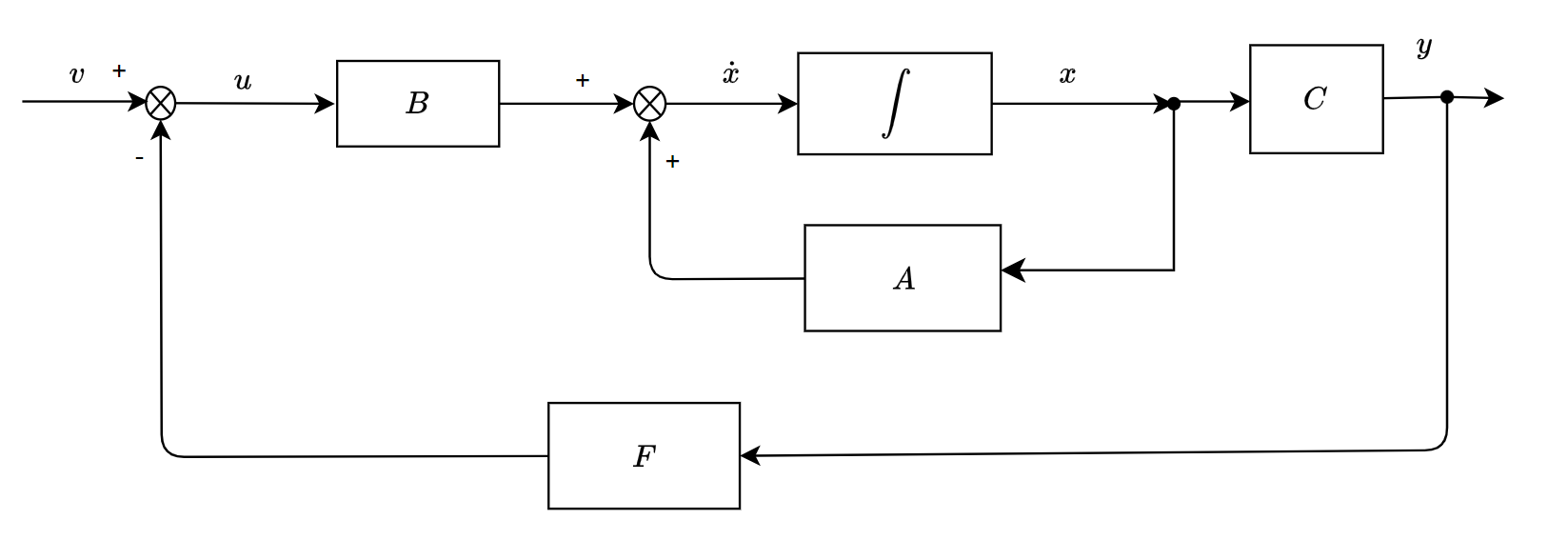
有: \[ \begin{equation} \begin{split} \dot{x}&=Ax+Bu\\ &=Ax+B(v-Fy)\\ &=Ax+B(v-FCx)\\ &=(A-BFC)x+Bv\\ y&=Cx \end{split} \end{equation} \] 特征多项式:\(\alpha(s)=det(sI-A+BFC)\)
传递函数矩阵:\(G_F(s)=C(sI-A+BFC)^{-1}B\)
(3)状态反馈和输出反馈的比较
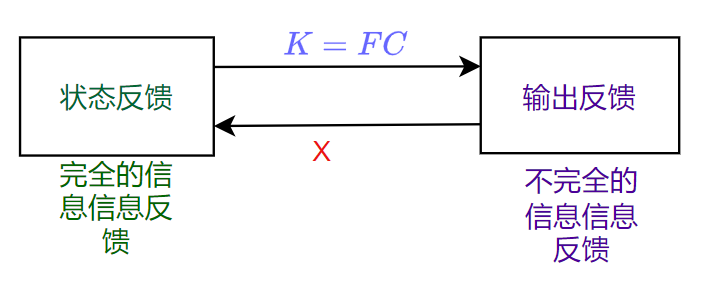
对于反馈功能:输出反馈能完成的任务,状态反馈一定能完成;反之不一定。
1.2 反馈结构对系统性能的影响
(1)对于系统能控性和能观测性
结论:状态反馈不改变系统能控性,但可能改变系统的能观测性。
当闭环反馈系统出现零极点对消,被消去的极点便是不可观测的。
(2)对系统稳定性(只总结了状态反馈镇定)
状态反馈和输出反馈都改变系统的特征值,从而影响系统的稳定性。
可镇定性:若采用反馈措施能使闭环系统稳定,则称该系统是反馈可镇定的。
状态反馈镇定
有线性定常受控系统:
\(\dot{x}=Ax+Bu\)
有\(x(0)=x_0\),\(t \geq 0\)
若可以找到反馈状态控制律:\(u=v-Kx\)
使得构成的反馈闭环系统:\(\dot{x}=(A-BK)x+Bv\)是渐进稳定的,即\((A-BK)\)的特征值均具有负实部,则称系统实现了状态反馈镇定。
使线性定常系统状态反馈镇定(状态反馈闭环反馈系统稳定)的必要条件:该线性定常系统的不能控部分是渐进稳定的。
| 线性定常系统是否完全能控 | 线性定常系统不能控部分是否渐进稳定 | 其状态反馈是否为可镇定 |
|---|---|---|
| 是 | 无不能控部分 | 是 |
| 否 | 是(不能控部分极点均具有负实部) | 是 |
| 否 | 否(不能控部分极点具有非负实部) | 否 |
2、状态反馈极点配置
2.1 极点配置问题的提法
| 连续时间线性时不变系统反馈方式 | 能否任意配置系统的全部极点 | 能否配置能控部分的极点 | 能否配置不能控部分的极点 | |
|---|---|---|---|---|
| 状态反馈 | 否 | 是 | 否 | |
| 输出反馈 | 否 | 是 | 否 | |
状态反馈极点配置的提法
连续时间线性时不变系统\(\dot{x}=Ax+Bu\)
给定\(n\)个期望闭环极点(即特征值)\({\lambda^{*}_1,\lambda^{*}_2,···,\lambda^{*}_n}\),试确定状态反馈矩阵\(K\),使得所得到的状态反馈闭环控制系统
\(\dot{x}=(A-BK)x+Bv\)
的特征值配置到期望极点处,即满足\(\lambda_i(A-BK)=\lambda_i^{*},i=1,2,3,···,n\)
注:状态反馈\(K\)不能改变不能控部分的极点,但能任意配置能控部分的极点
2.2 单输入系统状态反馈极点配置
2.2.1 利用状态反馈的极点可配置条件
结论1:利用状态反馈任意配置全部闭环极点(即特征值)的充分必要条件是被控系统完全能控。
结论2:如果系统不能控部分特征值属于期望闭环特征值,那仍能通过状态反馈配置系统的全部闭环极点。
对结论1的证明:以单输入-多输出系统来证明
充分性(系统完全能控\(=>\)状态反馈可任意配置闭环极点)证明:
设系统\((A,b)\)的特征多项式为: \[ \alpha(s)=det(sI-A)=s^n+\alpha_{n-1}^{n-1}s^{n-1}+···+\alpha_0 \] 如果系统完全能控,则可通过非奇异线性变换\(\overline{x}=P^{-1}x\)(即\(x=\overline{x}P\)),将其变换为可控标准型: \[ \dot{\overline{x}}=\overline{A}\overline{x}+\overline{b}u \]
\[ \begin{equation} \overline{A}= \begin{bmatrix} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & \dots & 0 & 1\\ -a_0 & -a_1 & -a_2 &\dots & -a_{n-1} \end{bmatrix}; \overline{b}=P^{-1}b= \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix} \end{equation} \]
矩阵\(\overline{A}\)对应的特征多项式(非奇异线性变换不改变原系统的特性): \[ det[sI-\overline{A}]=det[sI-A]=s^n+a_{n-1}s^{n-1}+\dots+a_1s+a_0 \] 设状态反馈矩阵: \[ \overline{k}= \begin{bmatrix} \overline{k}_1 & \dots & \overline{k}_n \end{bmatrix} \] 引入状态反馈后,闭环系统的状态方程为: \[ \dot{x}=(\overline{A}-\overline{b}K)x+\overline{b}v \] 引入状态反馈后,\((\overline{A}-\overline{b}K)\)的特征多项式为: \[ det[sI-(\overline{A}-\overline{b}K)]=s^n+(a_{n-1}+\overline{k}_n)s^{n-1}+\dots+(a_{1-1}+\overline{k}_2)s+(a_{0}+\overline{k}_1) \tag{1} \] 设期望的闭环系统特征值为\(\lambda_1^*、\lambda_2^*、\dots、\lambda_{n}^*\)
由期望闭环特征系统特征值确定的特征多项式: \[ \begin{equation} \begin{split} D(s)&=(s-\lambda_1^*)(s-\lambda_2^*)\dots(s-\lambda_n^*)\\&=s^n+a^*_{n-1}s^{n-1}+\dots+a^*_1s+a^*_0 \end{split} \end{equation} \tag{2} \] 比较公式(1)和公式(2)可得: \[ \begin{equation} \left\{ \begin{array}{lr} a_{n-1}+\overline{k}_n=a^*_{n-1}, & \\ \dots\\ a_{1}+\overline{k}_2=a^*_{1}, & \\ a_{0}+\overline{k}_1=a^*_{0} \end{array} \right. \end{equation} \] 可解得: \[ \begin{equation} \left\{ \begin{array}{lr} \overline{k}_n=a^*_{n-1}-a_{n-1}, & \\ \dots\\ \overline{k}_2=a^*_{1}-a_{1}, & \\ \overline{k}_1=a^*_{0}-a_{0} \end{array} \right. \end{equation} \] 故状态反馈阵为: \[ \overline{k}= \begin{bmatrix} a^*_0-a_0 & a^*_1a_1 & \dots & a^*_{n-1}-a_{n-1} \end{bmatrix} \] 对于原系统来说引入状态反馈可得到: \[ u=v-kx=v-kP\overline{x}=v-\overline{k}\overline{x} \] 即对于原系统使得闭环极点配置到\(\lambda_1^*、\lambda_2^*、\dots、\lambda_{n}^*\)的状态反馈矩阵: \[ k=\overline{k}P^{-1} \] 必要性(状态反馈可任意配置闭环极点\(=>\)系统完全能控)证明:
反证法:反设系统不完全能控,则不能控部分的状态不受输入\(u\)的影响与控制,引入状态反馈就不能通过控制\(k\)来改变不可控极点
2.3 单输入系统的极点配置算法
对给定\(n\)维受控系统\((A,b)\)和一组任意期望闭环特征值\(\lambda_1^*、\lambda_2^*、\dots、\lambda_{n}^*\),确定反馈增益矩阵\(k\),使得闭环系统矩阵\((A-bk)\)的特征值为\(\lambda_1^*、\lambda_2^*、\dots、\lambda_{n}^*\)
2.3.1 系数比较法
| 步骤 | 关键公式 |
|---|---|
| (1)计算期望特征多项式 | \(\alpha^*(s)=(s-\lambda^*_1)\dots(s-\lambda^*_n)\\=(s^n+\alpha^*_{n-1}s^{n-1}+\dots+\alpha^*_1s+\alpha^*_0)\) |
| (2)设\(k=\begin{bmatrix}k_1 & k_2 &\dots &k_n\end{bmatrix}\),用待定系数表示闭环系统的特征多项式 | \(alpha^(s)=det(sI-A+bk)\\=(s^n+\alpha_{n-1}s^{n-1}+\dots+\alpha_1s+\alpha_0)\) |
| (3)由上述两式得到方程组,解方程得到\(k\)矩阵中的元素 | \(\begin{equation}\left\{ \begin{array}{lr} a_{n-1}=a^*_{n-1}, & \\ \dots\\ a_{1}=a^*_{1}, & \\ a_{0}+=a^*_{0} \end{array}\right.\end{equation}\) |
2.3.2 完全能控单输入系统状态反馈极点配置的规范算法
| 步骤 | 关键公式 |
|---|---|
| (1)计算矩阵A的特征多项式 | \(\alpha(s)=det(sI-A)\\=(s^n+\alpha_{n-1}s^{n-1}+\dots+\alpha_1s+\alpha_0)\) |
| (2)计算期望特征多项式 | \(\alpha^*(s)=(s-\lambda^*_1)\dots(s-\lambda^*_n)\\=(s^n+\alpha^*_{n-1}s^{n-1}+\dots+\alpha^*_1s+\alpha^*_0)\) |
| (3)计算能控规范型反馈矩阵\(\overline{k}\) | \(k=\begin{bmatrix}\alpha^*_0-\alpha_0&\alpha^*_1-\alpha_1&\dots&\alpha^*_{n-1}-\alpha_{n-1}\end{bmatrix}\) |
| (4)计算非奇异变换矩阵\(P\) | \(P=\begin{bmatrix}A^{n-1}b &\dots & Ab & b\end{bmatrix}\begin{bmatrix}1 &\dots&0 & 0\\\alpha_{n-1} & 1 & \dots & 0\\\vdots & \vdots & \ddots & \vdots\\\alpha_{1}&\dots & \alpha_{n-1}&1\end{bmatrix}(左下三角)\\\)\(=\begin{bmatrix}b & Ab & \dots & A^{n-1}b\end{bmatrix}\begin{bmatrix}1 &\dots&0 & 0\\\alpha_{n-1} & 1 & \dots & 0\\\vdots & \vdots & \ddots & \vdots\\\alpha_{1}&\dots & \alpha_{n-1}&1\end{bmatrix}^T(左上三角)\) |
| (5)计算\(P^{-1}\) | \(P^{-1}=\frac{adj{P}}{det(P)}\) |
| (6)计算原系统的反馈增益阵 | \(k=\overline{k}P^{-1}\) |
2.3 状态反馈堆传递函数矩阵的影响
结论:
| 系统 | 结论 | |
|---|---|---|
| 单输入单输出线性定常系统 | 结论: 对完全能控\(n\)维单输入单输出线性时不变系统,引入状态反馈任意配置闭环系统传递函数极点的同时,零点一般不发生改变(如果状态反馈将闭环系统极点配置为与零点相重合,会产生对消零点的情况) | |
| 多输入多输出线性定常系统 | 结论:对完全能控的多输入多输出线性定常系统,状态反馈在配置传递函数矩阵全部\(n\)个极点的同时,一般不影响传递函数的零点 |