坐标变换旋转矩阵、四元数反解欧拉角公式推导
本文为对旋转矩阵的推导
坐标变换旋转矩阵、四元数反解欧拉角公式推导
author: LiaoYF
(以下内容带有很多我个人的理解,仅供参考,有错误的话也请指出)
本文中,以右手螺旋定则判断旋转角度的正负。
右手系的坐标系
一般的右手系定义中,大拇指指向是\(OZ\)轴,四指指向是\(OX\)轴,四指自然弯曲,从\(OX\)轴绕\(OZ\)轴向四指弯曲方向旋转90°是\(OY\)轴。
故无论\(X、Y、Z\)三轴朝向怎样,\(X、Y、Z\)三轴相对位置关系是一定的,所以当以一轴为旋转轴,对于剩下的二轴所在的二维平面来说旋转矩阵的形式是一定的。
假设旋转前的坐标系为\(a\),旋转后的坐标系为\(b\),该平面上有一点\(P\),则容易得到向量在\(b\)系下的坐标数值大小等于将\(\overrightarrow{OP}\)保持模长不变沿着反方向旋转相同角度在\(a\)系下的坐标数值。 与复数相乘具有几何意义,具体见下文。所以可用与复数相乘相似的方式来简单地推导出下列三个表达式。
一、二维平面的旋转矩阵
1、\(XOY\)平面上的坐标系进行旋转
\(XOY\)平面上的坐标系进行旋转,是绕垂直于\(XOY\)平面的轴旋转的,假设这个轴方向与右手系中的\(OZ\)轴方向(在图1.1中垂直于\(XOY\)平面向外)相同且过坐标原点,旋转角度为\(\theta\)。
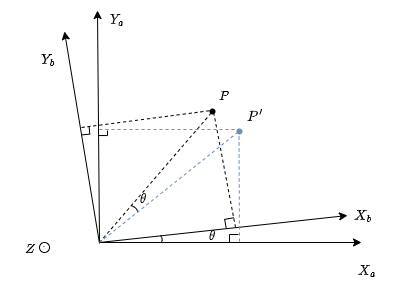
图1.1
假设\(Y\)轴是虚轴,\(X\)轴是实轴,复数\(Z_1 = x_{ap}+iy_{ap}\),复数\(Z_2 = x_{bp}+iy_{bp}\),复数\(Z_3 = e^{i(-\theta)}=cos\theta-isin\theta\)。
可由与复数相乘的几何意义得到下列式子1.1.2: \[ Z_2=Z_1Z_3 \tag{1.1.1} \]
\[ x_{bp}+iy_{bp}=(x_{ap}cos\theta+y_{ap}sin\theta) + i(-x_{ap}sin\theta+y_{ap}cos\theta) \tag{1.1.2} \]
可得到下列公式1.3 \[ \left[ \begin{array}{ccc} x_{bp} \\ y_{bp} \\ \end{array} \right] =\left[ \begin{array}{ccc} cos\theta & sin\theta \\ -sin\theta& cos\theta \\ \end{array} \right] \left[ \begin{array}{ccc} x_{ap} \\ y_{ap} \\ \end{array} \right] \tag{1.1.3} \]
2、\(XOZ\)平面上的坐标系进行旋转
\(XOZ\)平面上的向量旋转,是绕垂直于\(XOZ\)平面的轴旋转的,假设这个轴方向与右手系中的\(Y\)轴方向(在图1.2中垂直于\(XOZ\)平面向外)相同,旋转角度为\(\theta\)
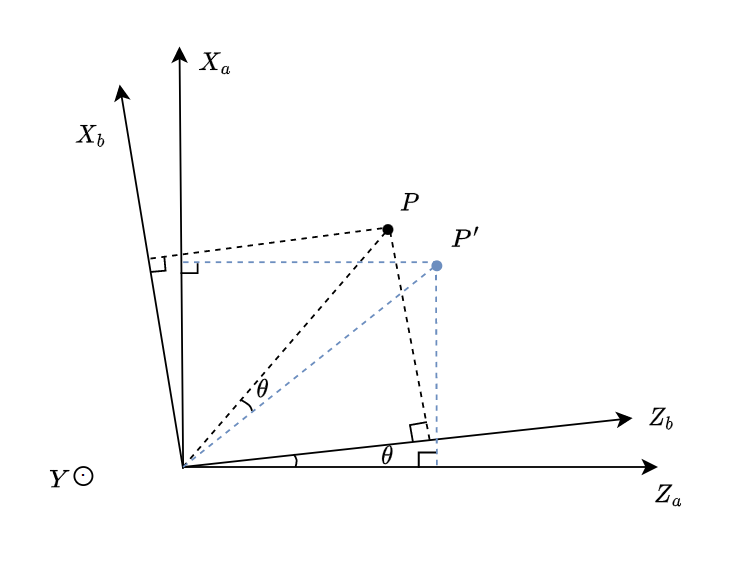
图1.2
假设X轴是虚轴,\(Z\)轴是实轴,复数\(Z_1 = z_{ap}+ix_{ap}\),复数\(Z_2 = z_{bp}+ix_{bp}\),复数\(Z_3 = e^{i(-\theta)}=cos\theta-isin\theta\)。
可由与复数相乘的几何意义得到下列式子1.2.1: \[ Z_2=Z_1Z_3 \]
\[ z_{bp}+ix_{bp}=(z_{ap}cos\theta+x_{ap}sin\theta) + i(-z_{ap}sin\theta+x_{ap}cos\theta) \tag{1.2.1} \]
可得到下列公式1.5 \[ \left[ \begin{array}{ccc} x_{bp} \\ Z_{bp} \\ \end{array} \right] =\left[ \begin{array}{ccc} cos\theta & -sin\theta \\ sin\theta& cos\theta \\ \end{array} \right] \left[ \begin{array}{ccc} x_{ap} \\ Z_{ap} \\ \end{array} \right] \tag{1.2.2} \]
3、\(YOZ\)平面上的坐标系进行旋转
\(YOZ\)平面上的向量旋转,是绕垂直于\(YOZ\)平面的轴旋转的,假设这个轴方向与右手系中的\(X\)轴方向(在图1.3中垂直于\(YOZ\)平面向外)相同,旋转角度为\(\theta\)
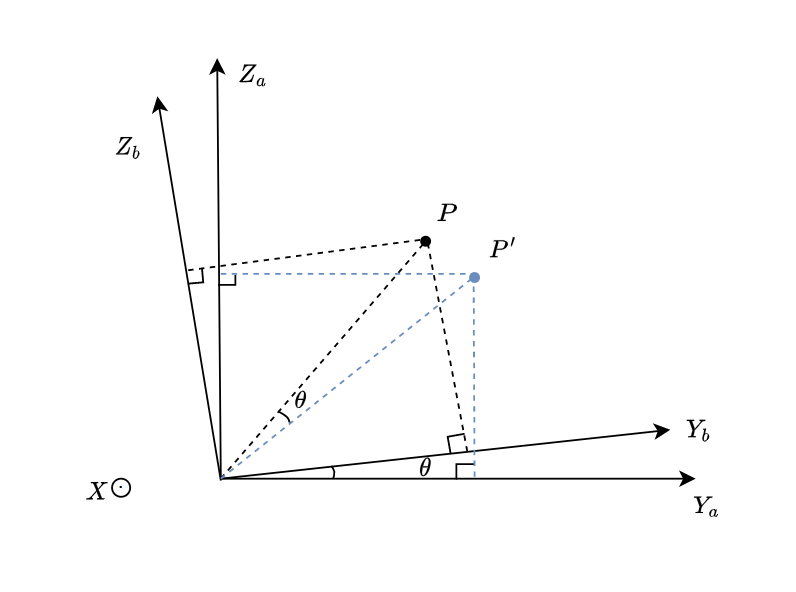
图1.3
假设Z轴是虚轴,Y轴是实轴,复数\(Z_1 = y_{ap}+iz_{ap}\),复数\(Z_2 = y_{bp}+iz_{bp}\),复数\(Z_3 = e^{i(-\theta)}=cos\theta-isin\theta\)。
可由与复数相乘的几何意义得到下列式子1.3.1: \[ Z_2=Z_1Z_3 \]
\[ y_{bp}+iz_{bp}=(y_{ap}cos\theta+z_{ap}sin\theta) + i(-y_{ap}sin\theta+z_{ap}cos\theta) \tag{1.3.1} \]
可得到下列公式1.7 \[ \left[ \begin{array}{ccc} y_{bp} \\ Z_{bp} \\ \end{array} \right] =\left[ \begin{array}{ccc} cos\theta & sin\theta \\ -sin\theta& cos\theta \\ \end{array} \right] \left[ \begin{array}{ccc} y_{ap} \\ Z_{ap} \\ \end{array} \right] \tag{1.3.2} \]
二、三维坐标系的旋转矩阵
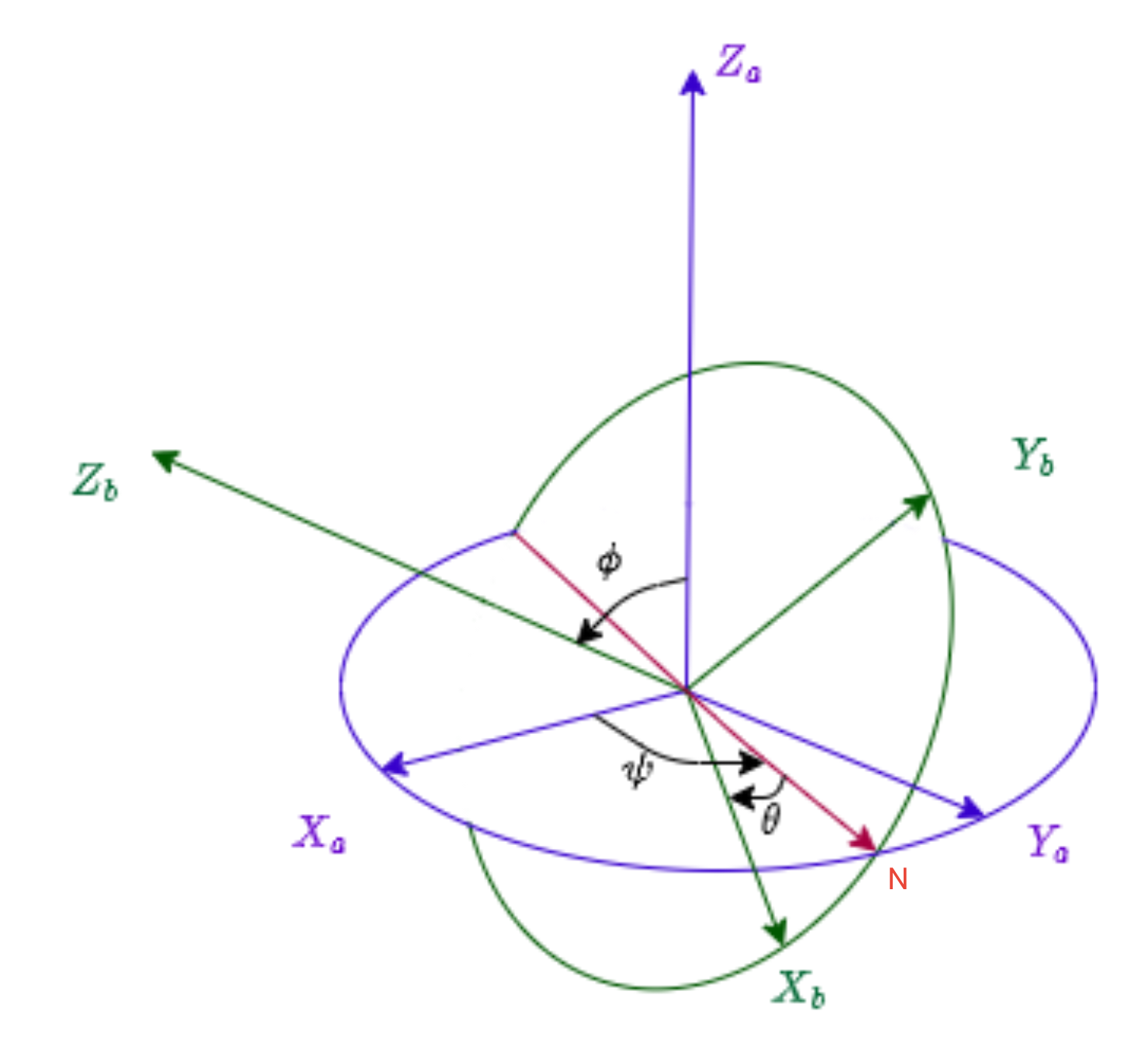
图2.1
1、本文所使用的三维坐标系假设
设坐标系\(OX_aY_aZ_a\)为固定坐标系,坐标系\(b\)是动坐标系。设坐标系\(b\)起始位置(\(OX_bY_bZ_b\))与坐标系\(OX_aY_aZ_a\)三轴方向平行,且坐标原点重合,坐标系\(b\)旋转之后为\(OX_b^{''}Y_b^{''}Z_b^{''}\)坐标系。假设坐标系\(OX_aY_aZ_a\)为三轴正交的坐标系,朝前是\(X_a\)轴,朝右是\(Y_a\)轴,朝上是\(Z_a\)轴。如图2.1所示,故可设任意时刻坐标系\(b\)相对于旋转轴旋转欧拉姿态角\(\psi、\theta、\phi\)(当\(OX_aY_aZ_a\)为地理坐标系,坐标系\(b\)为机体坐标系时,这三个角度分别对应航向角、俯仰角、横滚角),\(ON\)轴表示坐标系\(b\)第一次绕\(OZ_a(OZ_b)\)轴旋转之后的\(X_b'\)轴。
2、旋转顺序
一般从固定坐标到动坐标系到动坐标系需要经过三次旋转,每次旋转之后绕不同的轴再进行一次旋转。需满足每次旋转之后,绕旋转轴的角度能和欧拉角相匹配。
所以在“1、本文所使用的三维坐标系假设”条件下,应选择的旋转顺序为固定坐标系的\(Z->Y->X\),即先绕\(OZ_a(OZ_b)\)轴旋转\(\psi\),再绕\(OY_b'\)轴旋转\(\theta\),最后绕\(OX_b''\)轴旋转\(\phi\)。
3、旋转矩阵推导
已知:三坐标轴相互垂直的正交坐标系间相互变换的旋转矩阵为正交矩阵\(R(\theta)\),满足\(R(\theta)^{-1} = R(\theta)^{T}\)
设空间中存在一点\(P\),在坐标系\(OX_aY_aZ_a\)中可表示为\(P(x_{ap},y_{ap},z_{ap})\),在旋转之后的坐标系\(OX_b^{''}Y_b^{''}Z_b^{''}\)中可表示为\(P(x^{''}_{bp},y^{''}_{bp},z^{''}_{bp})\)
(1)第1次旋转
设坐标系\(b\)第一次绕\(OZ_a(OZ_b)\)轴旋转\(\psi\)之后的坐标系是\(OX_{b}'Y_b'Z_b\)
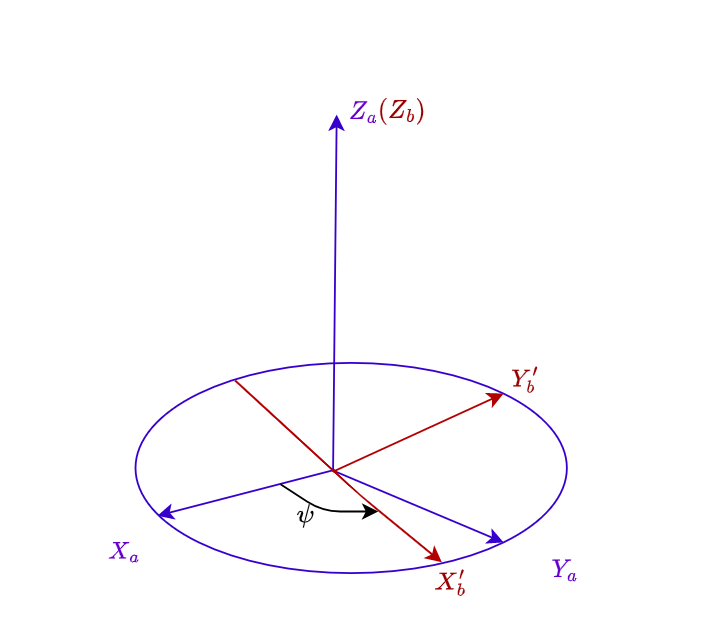
图2.2\[ \left[ \begin{array}{ccc} x^{'}_{bp} \\ y^{'}_{bp} \\ z_{ap} \end{array} \right] =\left[ \begin{array}{ccc} cos\psi & sin\psi & 0 \\ -sin\psi& cos\psi & 0\\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{ccc} x_{ap} \\ y_{ap} \\ z_{ap} \end{array} \right] \tag{2.3.1} \]
\[ R_z = \left[ \begin{array}{ccc} cos\psi & sin\psi & 0 \\ -sin\psi& cos\psi & 0\\ 0 & 0 & 1 \end{array} \right] \tag{2.3.2} \]
(2)第2次旋转
设坐标系\(b\)第2次绕\(OY^{'}_b\)轴旋转\(\theta\)之后的坐标系是\(OX^{''}_{b}Y^{'}_bZ^{'}_b\)
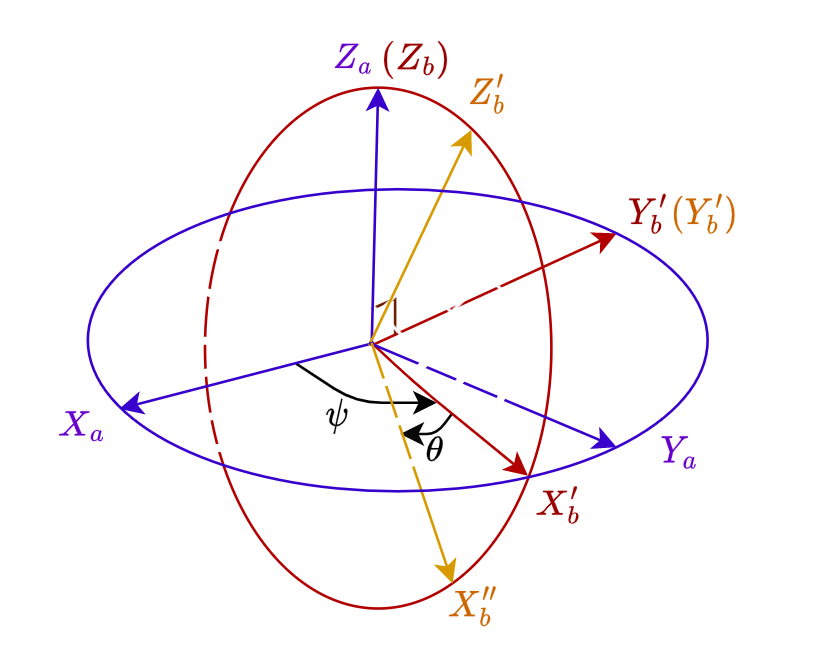
图2.3 \[ \left[ \begin{array}{ccc} x^{''}_{bp} \\ y^{'}_{bp} \\ z^{'}_{bp} \end{array} \right] =\left[ \begin{array}{ccc} cos\theta & 0& -sin\theta \\ 0 & 1 & 0\\ sin\theta& 0 & cos\theta \end{array} \right] \left[ \begin{array}{ccc} x^{'}_{bp} \\ y^{'}_{bp} \\ z_{ap} \end{array} \right] \tag{2.3.3} \]
\[ R_y=\left[ \begin{array}{ccc} cos\theta & 0& -sin\theta \\ 0 & 1 & 0\\ sin\theta& 0 & cos\theta \end{array} \right] \tag{2.3.4} \]
(3)第3次旋转
设坐标系\(b\)第3次绕\(OX^{''}_b\)轴旋转\(\phi\)之后的坐标系是\(OX^{''}_{b}Y^{''}_bZ^{''}_b\)
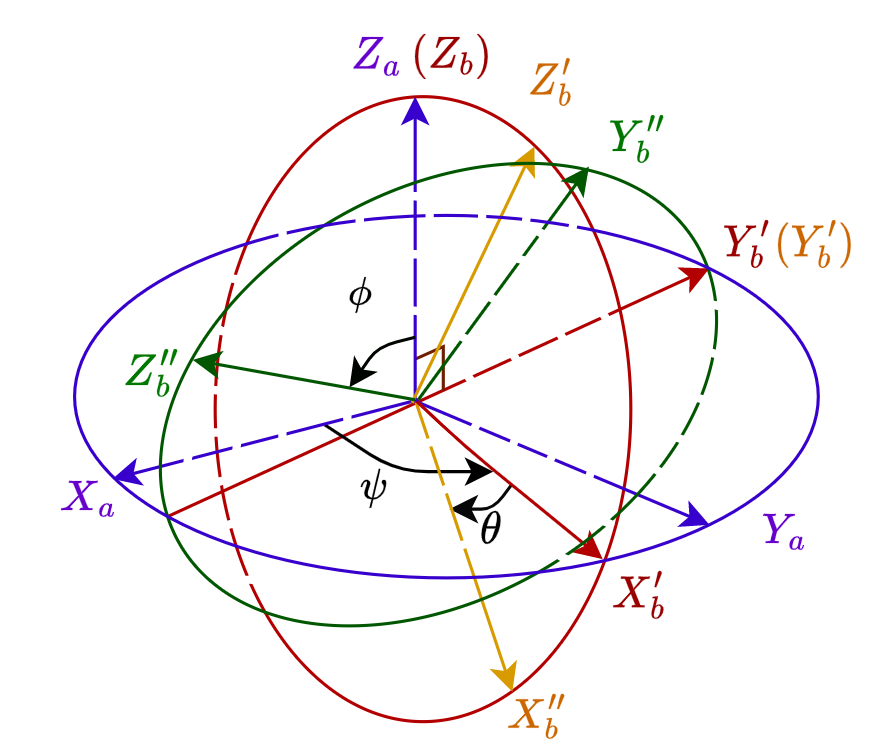
图2.4 \[ \left[ \begin{array}{ccc} x^{''}_{bp} \\ y^{''}_{bp} \\ z^{''}_{bp} \end{array} \right] =\left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & cos\phi & sin\phi \\ 0 & -sin\phi & cos\phi \end{array} \right] \left[ \begin{array}{ccc} x^{''}_{bp} \\ y^{'}_{bp} \\ z^{'}_{bp} \end{array} \right] \tag{2.3.5} \]
\[ R_x=\left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & cos\phi & sin\phi \\ 0 & -sin\phi & cos\phi \end{array} \right] \tag{2.3.6} \]
(4)坐标系\(OX_aY_aZ_a\)到坐标系\(OX_b^{''}Y_b^{''}Z_b^{''}\)的旋转矩阵
\[ \left[ \begin{array}{ccc} x^{''}_{bp} \\ y^{''}_{bp} \\ z^{''}_{bp} \end{array} \right] = C^b_a \left[ \begin{array}{ccc} x_{ap} \\ y_{ap} \\ z_{ap} \end{array} \right] \]
\[ C^b_a= R_xR_yR_z \tag{2.3.7} \]
\[ \begin{flalign} C^b_a &= \begin{bmatrix} cos (\psi )cos (\theta ) & cos (\theta )sin (\psi ) & -sin (\theta )\\ cos (\psi )sin (\phi )sin (\theta )-cos (\phi )sin (\psi ) & cos (\phi )cos (\psi )+sin (\phi )sin (\psi )sin (\theta ) & cos (\theta )sin (\phi )\\ sin (\phi )sin (\psi )+cos (\phi )cos (\psi )sin (\theta ) & cos (\phi )sin (\psi )sin (\theta )-cos (\psi )sin (\phi ) & cos (\phi )cos (\theta ) \end{bmatrix} \end{flalign} \tag{2.3.8} \]
(5)坐标系\(OX_b^{''}Y_b^{''}Z_b^{''}\)到坐标系坐标系\(OX_aY_aZ_a\)的旋转矩阵
\[ \left[ \begin{array}{ccc} x_{ap} \\ y_{ap} \\ z_{ap} \end{array} \right] = C^a_b\left[ \begin{array}{ccc} x^{''}_{bp} \\ y^{''}_{bp} \\ z^{''}_{bp} \end{array} \right] \]
\[ C^a_b= {(C^b_a)}^{(-1)}={(C^b_a)}^{T}=R^T_zR^T_yR^T_x\tag{2.3.9} \]
(此处公式超出界面了,之后会解决,抱歉) \[ C^a_b=\left[\begin{array}{ccc} \cos \left({\psi} \right)\cos \left({\theta} \right) & \cos \left({\psi} \right)sin \left({\phi} \right)sin \left({\theta} \right)-\cos \left({\phi} \right)sin \left({\psi} \right) & sin \left({\phi} \right)sin \left({\psi} \right)+\cos \left({\phi} \right)\cos \left({\psi} \right)sin \left({\theta} \right)\\ \cos \left({\theta} \right)sin \left({\psi} \right) & \cos \left({\phi} \right)\cos \left({\psi} \right)+sin \left({\phi} \right)sin \left({\psi} \right)sin \left({\theta} \right) & \cos \left({\phi} \right)sin \left({\psi} \right)sin \left({\theta} \right)-\cos \left({\psi} \right)sin \left({\phi} \right)\\ -sin \left({\theta} \right) & \cos \left({\theta} \right)sin \left({\phi} \right) & \cos \left({\phi} \right)\cos \left({\theta} \right) \end{array}\right]\tag{2.3.10} \]
三、欧拉角表示旋转的缺陷
欧拉角表示旋转存在万向锁问题
仍然以“二”中假设的坐标系为例,用欧拉角表示旋转时第2次旋转时\(|\theta|\)不能等于90°,下面以欧拉角的微分方程推导来说明原因。
假设坐标系\(b\)相对于坐标系\(OX_aY_aZ_a\)的角速度分别为\(\dot{\psi}\)、\(\dot{\theta}\)、\(\dot{\phi}\),假设这三个角速度矢量在坐标系\(b\)最终位置坐标系\(OX_b^{''}Y_b^{''}Z_b^{''}\)的轴向分量分别为\(\omega_{zb}、\omega_{yb}、\omega_{xb}\)
在坐标系\(b\)从初始位置旋转到坐标系\(OX_b^{''}Y_b^{''}Z_b^{''}\)的过程中:
进行第1次旋转后,得到了\(\dot{\psi}\),将其转换为\(\omega_{zb}\),还需最后2次的旋转矩阵来做变换: \[ \left[ \begin{array}{ccc} 0 \\ 0 \\ \omega_{zb} \end{array} \right] = R_xR_y\left[ \begin{array}{ccc} 0 \\ 0 \\ \dot{\psi} \end{array} \right] \tag{3.1} \] 进行第2次旋转时,得到了\(\dot{\theta}\),还需使用第3次的旋转矩阵来进行角速度的变换: \[ \left[ \begin{array}{ccc} 0 \\ \omega_{yb} \\ 0 \end{array} \right] = R_x\left[ \begin{array}{ccc} 0 \\ \dot{\theta} \\ 0 \end{array} \right]\tag{3.2} \] 进行第3次旋转时,容易得到: \[ \omega_{xb} = \dot{\phi} \tag{3.3} \] 由式3.1、3.2、3.3可得: \[ \left[ \begin{array}{ccc} \omega_{xb} \\ \omega_{yb}\\ \omega_{zb} \end{array} \right] = \left[\begin{array}{c} {\dot{\phi}} -sin \left(\theta \right)\,\dot{\psi} \\ \cos \left(\phi \right)\,\dot{\theta} +\cos \left(\theta \right)\,sin \left(\phi \right)\,\dot{\psi} \\ \cos \left(\phi \right)\,\cos \left(\theta \right)\,\dot{\psi} -sin \left(\phi \right)\,\dot{\theta} \end{array}\right] \]
\[ \left[ \begin{array}{ccc} \omega_{xb} \\ \omega_{yb}\\ \omega_{zb} \end{array} \right] = \left[ \begin{array}{ccc} 1 & 0 & -sin{(\theta)}\\ 0 & \cos{(\phi)} & \cos{(\theta)} sin{(\phi)}\\ 0 & -sin{(\phi)} & \cos{(\phi)}\cos{(\theta)} \end{array} \right] \left[ \begin{array}{ccc} \dot{\phi} \\ \dot{\theta}\\ \dot{\psi} \end{array} \right] \tag{3.4} \]
\[ \left[ \begin{array}{ccc} \dot{\phi} \\ \dot{\theta}\\ \dot{\psi} \end{array} \right]= \left[ \begin{array}{ccc} 1 & 0 & -sin{(\theta)}\\ 0 & \cos{(\phi)} & \cos{(\theta)} sin{(\phi)}\\ 0 & -sin{(\phi)} & \cos{(\phi)}\cos{(\theta)} \end{array} \right]^{-1} \left[ \begin{array}{ccc} \omega_{xb} \\ \omega_{yb}\\ \omega_{zb} \end{array} \right] \]
故可得: \[ \left[ \begin{array}{ccc} \dot{\phi} \\ \dot{\theta}\\ \dot{\psi} \end{array} \right]= \frac{1}{\cos{\theta}}\left[ \begin{array}{ccc} \cos{(\theta)} & sin{(\phi)}sin{(\theta)} & \cos{(\phi)}sin{(\theta)} \\ 0 & \cos{(\phi)}\cos{(\theta)} & -sin{(\phi)}\cos{(\theta)}\\ 0 & sin{(\phi)} & \cos{(\phi)} \end{array} \right] \left[ \begin{array}{ccc} \omega_{xb} \\ \omega_{yb}\\ \omega_{zb} \end{array} \right] \tag{3.5} \] 由方程3.5可得,\(|\theta|\)等于\(90°\)时,方程出现奇点。
四、四元数表示旋转
1、二维复平面中,与复数\(re^{i\beta}\)相乘的几何意义
设二维复平面中的一个复数\(r_{1}e^{i\beta}\),其对应的经过坐标原点的向量为$ \(,\)r_{1}e{i}\(与\)re{i}\(相乘意味着,\) \(模长变为原来的\)r\(倍,且绕坐标原点旋转\)$角度
2、四元数相乘也具有几何意义
假设一个纯四元数\(\hat{P} = (0,p_x,p_y,p_y)\),其可对应在三维空间中的一个向量。假设一个单位四元数\(\hat{q}=(q_0,q_1,q_2,q_3),q_0\)代表实部。 对于四元数有 \[ q^{-}=\frac{q^{*}}{|q|} \tag{4.2.1} \] 对于单位四元数有: \[ |q|=1 \tag{4.2.2} \] 故对单位四元数有: \[ q^{-}=q^{*} \tag{4.2.3} \]
(1)轴角表示旋转与四元数的关系
假设一个以单位向量定义的旋转轴\(\hat{u}=(ux,uy,uz)\),点\(v\)的坐标\((0,x_v,y_v,z_v)\)以该旋转轴右手系方向旋转\(\alpha\)角度后变为点\(v'\),\(\hat{q}=(q_0,q_1,q_2,q_3)\)为单位四元数,有以下关系式: \[ \hat{v'}=\hat{q}\hat{v}\hat{q}^{-}=\hat{q}\hat{v}\hat{q}^{*} \tag{4.2.4} \] 其中: \[ \hat{q}=(\cos\frac{\alpha}{2},\overrightarrow{u} sin\frac{\alpha}{2}) \tag{4.2.5} \]
(2)四元数表示旋转矩阵
将式4.2.4利用四元数乘法展开可得到四元数表示的旋转矩阵: \[ \begin{equation} \begin{split} \begin{bmatrix} x^{'}_v \\ y^{'}_v\\ z^{'}_v \end{bmatrix} &=\begin{bmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2) \\ 2(q_1q_2+q_0q_3) & 1-2(q_1^2+q_3^2) & 2(q_2q_3-q_0q_1) \\ 2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & 1-2(q_1^2+q_2^2) \end{bmatrix} \begin{bmatrix} x_v \\ y_v\\ z_v \end{bmatrix} \end{split} \end{equation} \tag{4.2.5} \] 其中: \[ q_0=\cos\frac{\alpha}{2},q_1=u_x sin\frac{\alpha}{2},q_2=u_y sin\frac{\alpha}{2},q_3=u_z sin\frac{\alpha}{2} \tag{4.2.6} \] 四元数旋转矩阵如下: \[ R = \left[ \begin{array}{ccc} 1-2(q_2^2+q_3^2) & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2) \\ 2(q_1q_2+q_0q_3) & 1-2(q_1^2+q_3^2) & 2(q_2q_3-q_0q_1) \\ 2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & 1-2(q_1^2+q_2^2) \end{array} \right] \tag{4.2.7} \]
(3)四元数反解欧拉角
当式4.2.7的旋转矩阵代表的是动坐标系到固定坐标系的旋转,且坐标系方向、角度定义与“二”中相同时,可通过与式2.3.10相比较,计算得到欧拉角大小。 \[ \frac{(C^a_{b})_{32}}{(C^a_{b})_{33}}=\tan\phi=\frac{b_{32}}{b_{33}}\\ (C^a_{b})_{31}=sin(-\theta) =b_{31}\\ \frac{(C^a_{b})_{21}}{(C^a_{b})_{11}}=\tan\psi=\frac{b_{21}}{b_{11}}\\ \]
\[ \theta = \mathrm{asin}\left(2\,q_0 \,q_2 -2\,q_1 \,q_3 \right)\tag{4.2.8} \]
\[ \phi = \textrm{atan2}\left(2\,q_0 \,q_1 +2\,q_2 \,q_3 ,-2\,{q_1 }^2 -2\,{q_2 }^2 +1\right)\tag{4.2.9} \]
\[ \psi = \textrm{atan2}\left(2\,q_0 \,q_3 +2\,q_1 \,q_2 ,-2\,{q_2 }^2 -2\,{q_3 }^2 +1\right) \tag{4.2.10} \]
可由单位四元数\(q_0^2+q_1^2+q_2^2+q_3^2=1\),变换出\(q_i^2\)和项的不同形式。